
No todos los estudiantes aprenden de la misma manera. A unos el estímulo visual les llega antes, a otros el auditivo, el táctil o el kinestésico. Si descubres qué tipo de aprendizaje sigues, podrás conseguir que tu rendimiento académico sea mayor y mejor.
EVAP 9: FORMULAS CON SUBPROCESOS
(MARTES)
//FORMULA DE LA FUERZA
SubProceso Fuerza1 <-FUERZA(m,a)
Fuerza1<-m*a;
FinSubProceso
//FORMULA DE LA RESISTENCIA DEL SONIDO
SubProceso Z <-RESISTENCIA_SONIDO(LAMDA,d)
Z<-20*Ln(LAMDA/(4*pi*d));
FinSubProceso
//FORMULA DE LA ATENUACION DEL SONIDO
SubProceso RETORNO <-ATENUACION_SONIDO(NPS,D,d1)
RETORNO<-NPS-20*Ln(D/d1);
FinSubProceso
//FORMULA DE NUMERO DE REYNOLDS
SubProceso N_REYNOLDS <-NUMERO_DE_REYNOLDS(v,D1,p,n)
N_REYNOLDS<-(v*D1*P)/n;
FinSubProceso
Proceso EJERCICIOS
//ELEGIR OPCION FORMULA
Escribir "***********MENU***********"
Escribir "1)FORMULA DE LA FUERZA"
Escribir "2)FORMULA DE LA RESISTENCIA DEL SONIDO"
Escribir "3)FORMULA DE LA ATENUACION DEL SONIDO"
Escribir "4)FORMULA DE NUMERO DE REYNOLDS"
Escribir "SELECCIONE UNA FORMULA:"
Leer opciones
Segun opciones Hacer
1:
//INICIO
Escribir "FORMULA DE LA FUERZA";
Escribir "______________________";
//DECLARACION
Definir R,Z, m, a, F como Real;
//ASIGNACION
Escribir "INGRESE LA MASA:";
Leer m;
Escribir "INGRESE LA ACELERACION:";
Leer a;
//PROCESO
R<-Fuerza(m,a);
//RESULTADO
Escribir "LA FUERZA ES:", R;
//FIN
2:
//INICIO
Escribir "2)FORMULA DE LA RESISTENCIA DEL SONIDO"
Escribir "________________________________________"
//DECLARACION
Definir PL, LAMDA, d, a como Real;
//ASIGNACION
Escribir "INGRESE LA ONDA LAMDA:"
Leer LAMDA;
Escribir "INGRESE LA DISTANCIA:"
Leer d;
R<-RESISTENCIA_SONIDO(LAMDA,d)
//RESULTADO
Escribir "LA RESISTENCIA DEL SONIDO ES:", R;
//FIN
3:
//INICIO
Escribir "FORMULA DE LA ATENUACION DEL SONIDO"
Escribir "________________________________________"
//DECLARACION
Definir R ,AT ,NPS ,D ,d1 como Real;
//ASIGNACION
Escribir "INGRESE EL NUMERO DE PULSOS:"
Leer NPS;
Escribir "INGRESE EL DIAMETRO MAYOR:"
Leer D;
Escribir "INGRESE EL DIAMETRO MENOR:"
Leer d1;
R<-ATENUACION_SONIDO(NPS,D,d1)
//RESULTADO
Escribir "LA ATENUACION DEL SONIDO ES:", R;
//FIN
4:
//INICIO
Escribir "FORMULA DE NUMERO DE REYNOLDS"
Escribir "__________________________________"
//DECLARACION
Definir NR, v, D1, P, n como Real;
//ASIGNACION
Escribir "INGRESE LA VELOCIDAD DEL FLUIDO:"
Leer v;
Escribir "INGRESE EL DIAMETRO DEL TUBO:"
Leer D1;
Escribir "INGRESE LA DENSIDAD DEL FLUIDO:"
Leer p;
n<- 0.001
Escribir "Coeficiente de Viscocidad del Agua a 20°:", n;
NR<-NUMERO_DE_REYNOLDS(v,D1,p,n)
//RESULTADO
Escribir "EL NUMERO DE REYNOLDS ES:", NR;
//FIN
De Otro Modo:
Escribir "NO HA SELECCIONADO UNA FORMULA"
Fin Segun
FinProceso
//FIN
EVAP 9: FORMULAS CON FUNCIONES
(JUEVES)
//FORMULA DE LA EFICIENCIA VOLUMETRICA
SubProceso E_VOL<-EFIC_VOL(v2,v1,vd)
E_VOL<-(v2-v1)/vd
FinSubProceso
//ECUACION CUADRATICA DE X
SubProceso E_C <-ECUAC_CUADRATICA(Rad)
E_c<-sen(Rad)+2*(cos(Rad))^2;
FinSubProceso
//FORMULA DE FUERZA ELECTRICA
SubProceso F_ELECTRICA<-FUERZA_ELECTRICA(K,q1,q2,r)
F_ELECTRICA<-(K*abs(q1*q2))/(r)^2;
FinSubProceso
//FORMULA DE CAMPO ELECTRICO
SubProceso C_ELECTRICO<-CAMPO_ELECTRICO(K,r,q)
C_ELECTRICO<-(K*q)/(r)^2;
FinSubProceso
Proceso EJERCICIOS
//ELEGIR OPCION FORMULA
Escribir "***********MENU***********"
Escribir "1)FORMULA DE LA EFICIENCIA VOLUMETRICA"
Escribir "2)ECUACION CUADRATICA"
Escribir "3)FORMULA DE LA FUERZA ELECTRICA"
Escribir "4)PLANTEADO:FORMULA DE CAMPO ELECTRICO"
Escribir "SELECCIONE UNA FORMULA:"
Leer opciones
Segun opciones Hacer
1:
//INICIO
Escribir "FORMULA DE LA EFICIENCIA VOLUMETRICA"
Escribir "________________________________________"
//DECLARACION
Definir EV, v1, v2, vd como Real;
//ASIGNACION
Escribir "INGRESE EL VOLUMEN 2:"
Leer v2;
Escribir "INGRESE EL VOLUMEN 1:"
Leer v1;
Escribir "INGRESE EL VOLUMEN DIFERENCIAL:"
Leer vd;
EV<-EFIC_VOL(v2,v1,vd)
//RESULTADO
Escribir "LA EFICIENCIA VOLUMETRICA ES:",EV;
//FIN
2:
//INICIO
Escribir "ECUACION CUADRATICA DE X";
Escribir "______________________________";
Escribir "LA ECUACION ES: F(x)=Sen(x)+2*(Cos(x)^2)"
//DECLARACION
Definir rad, rad1, F_x,x como Real;
//ASIGNACION
Escribir "INGRESE EL VALOR DE X:";
Leer x;
//PROCESO
Rad=(2*PI*x)/360
F_x<-ECUAC_CUADRATICA(Rad);
//RESULTADO
Escribir "EL RESULTADO DE LA ECUACION CUADRATICA ES DE X ES F(X):", F_x;
//FIN
3:
//INICIO
Escribir "FORMULA DE LA FUERZA ELECTRICA"
Escribir "__________________________________"
//DECLARACION
Definir FE, F, K, q1, q2, r como Real;
//ASIGNACION
Escribir "INGRESE LA CARGA 1:"
Leer q1;
Escribir "INGRESE LA CARGA 2:"
Leer q2;
Escribir "INGRESE LA DISTANCIA ENTRE CARGAS:"
Leer r;
K<- 9*(10)^9
Escribir "La Constante Electrostatica es:", K;
FE<-FUERZA_ELECTRICA(K,q1,q2,r)
//RESULTADO
Escribir "EL FUERZA ELECTRICA ES:", FE;
//FIN
4:
//INICIO
Escribir "PLANTEADO:FORMULA DE CAMPO ELECTRICO"
Escribir "__________________________________"
//DECLARACION
Definir CE, E, K, q, r como Real;
//ASIGNACION
Escribir "INGRESE LA DISTANCIA DE LA CARGA A PUNTO DE REFERENCIA:"
Leer r;
Escribir "INGRESE LA CARGA:"
Leer q;
K<- 9*(10)^9
Escribir "La Constante Electrostatica es:", K;
CE<-CAMPO_ELECTRICO(K,r,q)
//RESULTADO
Escribir "EL CAMPO ELECTRICO ES:", CE;
De Otro Modo:
Escribir "NO HA SELECCIONADO UNA FORMULA"
Fin Segun
FinProceso
//FIN
ENSAYO DE INFORME
DE INVESTIGACION
"LEY DE GAUSS (FLUJO DE CAMPO ELECTRICO)"
-
INTRODUCCION
El presente trabajo de investigación presenta conceptos teóricos, fundamentación mediante fórmulas del teorema de Gauss tema ligado a mi estudio de Ingeniería Electrónica, el cual he venido trabajando en conjunto con otras fórmulas nuevas para mi conocimiento, por lo cual en la siguiente busco comprender y dar a entender de igual manera de lo que trata la Ley de Gauss.
2. OBJETIVOS
Los objetivos principales de este informe son los siguientes:
-
Dar a comprender el Teorema o Ley de Gauss.
-
Explicar el método de empleo de la fórmula de la ley para la realización de algoritmos y Diagramas de Flujos.
-
Demostración de la ejecución de la formula en un pseudocódigo en el software Pseint, además de adjuntar su respectivo diagrama.
-
Demostrar mis conocimientos de los comandos, funciones o subprogramas y estructura de datos de fórmulas en Pseint.
3. ALCANCE
El tema que acapara el presente informe es el tema de la Ley de Gauss que nos informa respecto al flujo de campo en superficie cerrada y su relación con otras magnitudes, que será detallado en el Marco Teórico.
4. JUSTIFICACION
El tema es de suma importancia ya que es uno de los principales desarrollados en la física básica para el estudio de la Electrónica, por lo cual nos brinda información muy útil en especial a estudiantes que recién comienzan la carrera o que ya están adentrándose mucho más.
5. MARCO TEORICO
En física la ley de Gauss, relacionada con el Teorema de la divergencia o Teorema de Gauss, establece que el flujo de ciertos campos a través de una superficie cerrada es proporcional a la magnitud de las fuentes de dicho campo que hay en el interior de la misma superficie. Estos campos son aquellos cuya intensidad decrece como la distancia a la fuente al cuadrado. La constante de proporcionalidad depende del sistema de unidades empleado.
Se aplica al campo electrostático y al gravitatorio. Sus fuentes son la carga eléctrica y la masa, respectivamente. También puede aplicarse al campo magnetostático.
La ley fue formulada por Carl Friedrich Gauss en 1835, pero no fue publicado hasta 1867. Es una de las cuatro ecuaciones de Maxwell, que forman la base de electrodinámica clásica, que relaciona el campo eléctrico con sus fuentes, las cargas. La ley de Gauss puede ser utilizada para obtener la ley de Coulomb, y viceversa.
La ley de Gauss nos permite calcular de una forma simple el módulo del campo eléctrico, cuando conocemos la distribución de cargas con simetría esférica o cilíndrica tal como veremos en esta página.
El flujo del campo eléctrico a través de cualquier superficie cerrada es igual a la carga q contenida dentro de la superficie, dividida por la constante ε0.
La superficie cerrada empleada para calcular el flujo del campo eléctrico se denomina superficie gaussiana.
Flujo del campo eléctrico
El flujo del campo eléctrico se define de manera análoga al flujo de masa. El flujo de masa a través de una superficie S se define como la cantidad de masa que atraviesa dicha superficie por unidad de tiempo.

El campo eléctrico puede representarse mediante unas líneas imaginarias denominadas líneas de campo y, por analogía con el flujo de masa, puede calcularse el número de líneas de campo que atraviesan una determinada superficie. Conviene resaltar que en el caso del campo eléctrico no hay nada material que realmente circule a través de dicha superficie.

Como se aprecia en la figura anterior, el número de líneas de campo que atraviesan una determinada superficie depende de la orientación de esta última con respecto a las líneas de campo. Por tanto, el flujo del campo eléctrico debe ser definido de tal modo que tenga en cuenta este hecho.
7. MARCO CONCEPTUAL
Vocabulario:
-
Carga: En electricidad, se denomina carga a cualquier componente de un circuito (resistencia, motor, equipo electrónico, etc.) que ofrece una mayor o menor resistencia al paso de la corriente, por lo que al conectarse a una fuente de fuerza electromotriz se considera como una "carga" o consumidor de energía eléctrica. Junto a las fuentes de alimentación, y el cableado forman los tres elementos básicos de todo circuito eléctrico. La carga también se puede definir como la impedancia de entrada de un circuito.
-
Campo eléctrico: El campo eléctrico (región del espacio en la que interactúa la fuerza eléctrica) es un campo físico que se representa por medio de un modelo que describe la interacción entre cuerpos y sistemas con propiedades de naturaleza eléctrica.
-
Superficie gaussiana: Definiremos una superficie gaussiana como cualquier superficie cerrada imaginaria que empleamos en la ley de Gauss, para calcular el campo el eléctrico debido a una cierta distribución de cargas.
-
Permitividad: La permitividad (llamada también constante dieléctrica) es una constante física que describe cómo un campo eléctrico afecta y es afectado por un medio. La permitividad del vacío es 8,8541878176x10-12 C2 / N·m2.
-
Flujo Electrico: En electromagnetismo el flujo eléctrico, o flujo electrostático, es una magnitud escalar que expresa una medida del campo eléctrico que atraviesa una determinada superficie, o expresado de otra forma, es la medida del número de líneas de campo eléctrico que penetran una superficie. Su cálculo para superficies cerradas se realiza aplicando la ley de Gauss. Por definición el flujo eléctrico parte de las cargas positivas y termina en las negativas, y en ausencia de las últimas termina en el infinito.
-
Campo Vectorial: En matemáticas, un campo vectorial representa la distribución espacial de una magnitud vectorial. Es una expresión de cálculo vectorial que asocia un vector a cada punto en el espacio euclidiano, de la forma.
-
Densidad de Carga: Se llama densidad de carga eléctrica a la cantidad de carga eléctrica por unidad de longitud, área o volumen que se encuentra sobre una línea, una superficie o una región del espacio, respectivamente. Por lo tanto se distingue en estos tres tipos de densidad de carga. Se representaría con las letras griegas lambda (λ), para densidad de carga lineal, sigma (σ), para densidad de carga superficial y ro (ρ), para densidad de carga volumétrica.
-
Densidad superficial de carga: Cantidad de carga por unidad de superficie.
Para aplicar la ley de Gauss es necesario conocer previamente la dirección y el sentido de las líneas de campo generadas por la distribución de carga. La elección de la superficie gaussiana dependerá de cómo sean estas líneas.
El flujo eléctrico total fuera de una superficie cerrada es igual a la carga encerrada, dividida por la permitividad.

El flujo eléctrico a través de un área, se define como el campo eléctrico multiplicado por el área de la superficie proyectada sobre un plano perpendicular al campo. La ley de Gauss es una ley general, que se aplica a cualquier superficie cerrada. Es una herramienta importante puesto que nos permita la evaluación de la cantidad de carga encerrada, por medio de una cartografía del campo sobre una superficie exterior a la distribución de las cargas. Para geometrías con suficiente simetría, se simplifica el cálculo del campo eléctrico.
La ley de Gauss permite la evaluación del campo eléctrico en muchas situaciones prácticas, mediante la formación de superficies gaussianas simétricas alrededor de una distribución de cargas y la evaluación del flujo eléctrico a través de esa superficie.
Otra forma de visualizar esto es considerar una sonda de área A, que puede medir el campo eléctrico perpendicular a esa área. Si se escoge cualquier trozo de superficie cerrada y realizamos sobre esa superficie la medida del campo perpendicular, al multiplicarlo por su área, obtendremos una medida de la carga eléctrica neta dentro de esa superficie, sin importar como está configurada esa carga interna.

Flujo Eléctrico
El concepto de flujo eléctrico es de utilidad en la asociación con la ley de Gauss. El flujo eléctrico a través de un área plana se define como el campo eléctrico multiplicado por la componente del área perpendicular al campo. Si el área no es plana, entonces la evalución del flujo requiere generalmente una integral de área puesto que el ángulo estará cambiando continuamente.


Cuando se usa el área A en una operación vectorial como esta, se entiende que la magnitud del vector es igual al área y la dirección del vector es perpendicular al área.
Campo creado por un plano infinito
El campo eléctrico creado por un plano infinito cargado puede ser calculado utilizando la ley de Gauss.
En la siguiente figura se ha representado un plano infinito cargado con una densidad superficial de carga σ (= q/S) uniforme y positiva. Las líneas de campo siempre salen de las cargas positivas, por lo que el campo creado por el plano será uniforme (ya que la densidad de carga lo es) y sus líneas irán hacia afuera de ambos lados del plano.

El flujo del campo eléctrico a través de cualquier superficie cerrada es siempre el mismo (ley de Gauss); en este caso, por simplicidad de cálculo, se ha elegido una superficie gaussiana cilíndrica (representada en rojo en la figura).
El flujo a través de la superficie lateral del cilindro es nulo (ninguna línea de campo la atraviesa). Las únicas contribuciones no nulas al flujo son las que se producen a través de sus dos bases. El flujo del campo eléctrico a través del cilindro es entonces:

Como las dos bases del cilindro son iguales y el módulo del campo es el mismo en todos los puntos de su superficie, la integral anterior se simplifica, quedando:

El valor del flujo viene dado por la ley de Gauss:

Y q/S es la densidad superficial de carga σ:

Interpretación
La ley de Gauss puede ser utilizada para demostrar que no existe campo eléctrico dentro de una jaula de Faraday. La ley de Gauss es la equivalente electrostática a la ley de Ampère, que es una ley de magnetismo. Ambas ecuaciones fueron posteriormente integradas en las ecuaciones de Maxwell.
Esta ley puede interpretarse, en electrostática, entendiendo el flujo como una medida del número de líneas de campo que atraviesan la superficie en cuestión. Para una carga puntual este número es constante si la carga está contenida por la superficie y es nulo si está fuera (ya que hay el mismo número de líneas que entran como que salen). Además, al ser la densidad de líneas proporcional a la magnitud de la carga, resulta que este flujo es proporcional a la carga, si está encerrada, o nulo, si no lo está.
Cuando tenemos una distribución de cargas, por el principio de superposición, sólo tendremos que considerar las cargas interiores, resultando la ley de Gauss.
Sin embargo, aunque esta ley se deduce de la ley de Coulomb, es más general que ella, ya que se trata de una ley universal, válida en situaciones no electrostáticas en las que la ley de Coulomb no es aplicable.
Aplicaciones de la Ley de Gauss
La ley de Gauss es una herramienta poderosa para el cálculo de los campos eléctricos cuando son originados por una distribución de cargas con suficiente simetría para poderse aplicar.

Si la distribución de cargas adolece de la simetría necesaria para aplicarle la ley de Gauss, entonces el campo debe obtenerse, sumando los campos de carga puntuales de los elementos de carga individuales. Ejemplos de estos:
Campo en el interior de un condensador
Un condensador o capacitor es un dispositivo formado por dos conductores (denominados armaduras), generalmente con forma de placas, cilindros o láminas, separados por el vacío o por un material dieléctrico (no conduce la electricidad), que se utiliza para almacenar energía eléctrica.
La forma más sencilla de un condensador consiste en dos placas metálicas muy cercanas entre sí con cargas q en una y -q en la otra. Este tipo de condensador se denomina plano-paralelo.
El módulo del campo eléctrico creado por cada una de las placas del condensador, como se ha visto en el ejemplo anterior, viene dado por:

Las líneas del campo eléctrico creado por la placa cargada positivamente están dirigidas hacia fuera de la misma, lo contrario que ocurre para la placa con carga negativa.

Por tanto, en el exterior del condensador el campo es nulo y en el interior su módulo es el doble del campo que crearía una sola de las placas:

8. MARCO PROCEDIMENTAL
Para el desarrollo del Algoritmo y Diagrama de Flujo, y posterior pseudocódigo se empleara la FORMULA DEL FLUJO ELECTRICO, proveniente de la Ley de Gauss.


8.1. ANALISIS: El paso inicial para el desarrollo del Pseudocódigo, Algoritmo y Diagrama de Flujo, es el análisis de la formula a emplear:
IDENTIFICACION DE VARIABLES:
= Flujo Eléctrico = Campo Eléctrico
= Área = Angulo entre E y A
REPRESENTACION DE VARIABLES: En el Algoritmo, Diagrama de Flujo y Pseudocódigo se debe tomar las variables con palabras del abecedario o terminar unidos por “_” en los espaciados, pero no son admitidos símbolos, pero para una mejor comprensión en este desarrollo se representaran las variables con abreviaturas de su significado.
= Flu_Elec = Camp_Elect
= Area = Ang_E_A
-
Rad=Para la conversión del Angulo entre E y A a radianes (magnitud aceptada en el software Pseint).
REPRESENTACION DE LA FORMULA:
Flu_Elect<-Camp_Elect*Area*Cos(Rad)
Términos para la Función:
-
Flujo_Elect= Para invocar
-
FE=Para transportar la respuesta
8.2. ALGORITMO: A continuación se presenta el algoritmo desarrollado empleando funciones.
1) Inicio: del Algoritmo
2) Declaración: de la Representación de las Variables
Flujo_Elect, Flu_Elec, Camp_Elect, Area, Ang_E_A <-Real
3) Asignacion: de las Variables
Leer (Camp_Elect,Area,Ang_E_A)
4) Proceso: de la formula y función
Rad<-(2*PI*Ang_E_A)/360
Flu_Elect<-Flujo_Elect(Camp_Elect, Area, Rad)//Invocacion
5) Resultado:
Escribir (Flu_Elect) //Respuesta
6) FIN
// Zona de Funciones
Flujo_Elect(Camp_Elect, Area, Rad)<-Real
FE<- Camp_Elect*Area*Cos(Rad) //Desarrolo
Retornar (FE) //Envía a 5) Resultado
8.3. PSEUDOCODIGO: En el software Pseint, aquí las funciones son denominadas por el comando “SubProceso”.
//FORMULA DEL FLUJO ELECTRICO
SubProceso FE<-FLUJO_ELECT(Camp_Elect,Area,Rad)
FE<-Camp_Elect*Area*Cos(Rad)
FinSubProceso
Proceso FORMULA_DEL_FLUJO_ELECTRICO
//INICIO
Escribir "FORMULA DE LA EFICIENCIA VOLUMETRICA"
Escribir "________________________________________"
//DECLARACION
Definir FLU_ELECT, rad, Camp_Elect, Area, Ang_E_A como Real;
//ASIGNACION
Escribir "INGRESE EL CAMPO ELECTRICO:"
Leer Camp_Elect;
Escribir "INGRESE EL AREA:"
Leer Area;
Escribir "INGRESE EL ANGULO ENTRE EL CAMPO ELECTRICO Y EL AREA:"
Leer Ang_E_A;
//PROCESO
Rad<-(2*PI*Ang_E_A)/360
FLU_ELECT<-FLUJO_ELECT(Camp_Elect,Area,Rad)
//RESULTADO
Escribir "EL FLUJO ELECTRICO ES:",FLU_ELECT;
//FIN
FinProceso
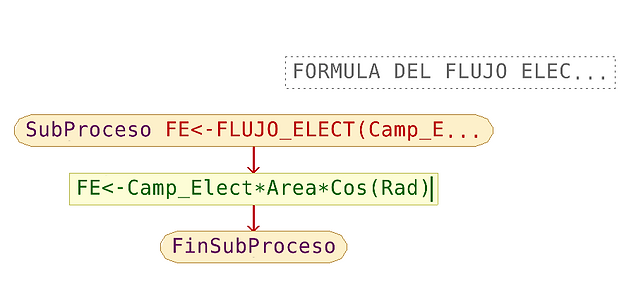
8.3. DIAGRAMA DE FLUJO: Esquema grafica del pseudocodigo en el software Pseint.

9. CONCLUSIONES
-
Finalmente, luego de concluido este trabajo de investigación puedo concluir que al menos la mayoría de las formulas matemáticas-físicas (ya que no conozco todas) puede ser adaptadas o representadas de manera que puedan ser empleadas para algoritmos informáticos, luego desarrollando una estructura, organizando las variables y dando una estructura con los datos obtenidos al algoritmo que se desea.
-
A sido muy útil aprovechar fórmulas de nuestra carrera Electrónica para poder desarrollar estos algoritmos ya que vamos aprendiendo muchas más nuevas fórmulas y comprendiendo su funcionamiento.
10. WEBGRAFIA
-
http://www2.montes.upm.es/dptos/digfa/cfisica/electro/gauss.html
-
https://es.wikipedia.org/wiki/Ley_de_Gauss#Flujo_del_campo_el%C3%A9ctrico
-
http://hyperphysics.phy-astr.gsu.edu/hbasees/electric/gaulaw.html
-
http://www.sc.ehu.es/sbweb/fisica3/electrico/gauss/gauss.html
-
https://es.wikipedia.org/wiki/Carga_el%C3%A9ctrica#Densidad_de_carga_el%C3%A9ctrica
-
https://www.youtube.com/watch?v=XRxn7ClTh6U (VIDEO EXPLICATIVO DIDACTICO)
